

Nächste Seite: Programmierung
Aufwärts: Dynamik von Defekten in
Vorherige Seite: Material und Methoden
Unterabschnitte
Nach dem Aufbau der Apparatur habe ich mit Messungen an Lipidmembranen aus
reinem DPh-PC begonnen. Dieses System wählte ich aus, da
mit [36,18,40] Vergleichsdaten vorhanden sind, um Meßaufbau
und die Durchführung der Experimente zu überprüfen.
Die Abbildungen 12-14 stellen den Verlauf einer Messung an
einer einzelnen Membran dar. Vor dem Aufnehmen der Spannungskurve zum
irreversiblen Durchbruch der Membranen wurde die Kapazität der Membran
bestimmt. Sie wird in die folgenden Berechnungen als Konstante eingesetzt.
Abbildung 12:
Entladungskurve DPh-PC Membran
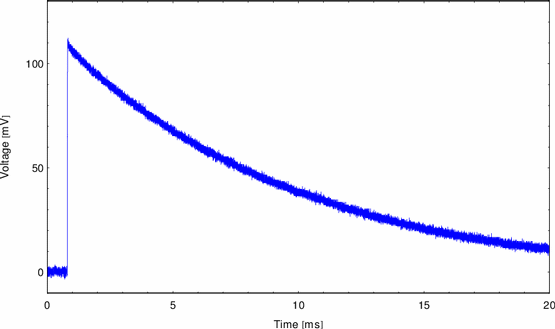 |
In Abbildung 12 betrug der Parallelwiderstand 10M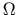 , der
Elektrolyt bestand aus 1M KCl. Die Kurve zeigt das Verhalten eines RC-Gliedes
mit 0,93nF als Kapazität des Kondensators. Die Kapazitätsmessung diente
zusätzlich der Qualitätskontrolle. Zu kleine Kapazitäten weisen auf nicht
zum Bilayer ausgedünnte Teile des Lipidfilmes hin. Wenn die Werte nach einer
gewissen Wartezeit nicht im Bereich der üblichen 0,8nF bis 1,2nF lagen, wurde
das Experiment mit einer neuen Membran wiederholt.
, der
Elektrolyt bestand aus 1M KCl. Die Kurve zeigt das Verhalten eines RC-Gliedes
mit 0,93nF als Kapazität des Kondensators. Die Kapazitätsmessung diente
zusätzlich der Qualitätskontrolle. Zu kleine Kapazitäten weisen auf nicht
zum Bilayer ausgedünnte Teile des Lipidfilmes hin. Wenn die Werte nach einer
gewissen Wartezeit nicht im Bereich der üblichen 0,8nF bis 1,2nF lagen, wurde
das Experiment mit einer neuen Membran wiederholt.
Abbildung 13 zeigt eine typische Meßkurve zum irreversiblen
Aufreißen der Lipiddoppelschicht bei Pulsspannungen über dem kritischen Wert.
Abbildung 13:
Durchbruch DPh-PC in 1M KCl
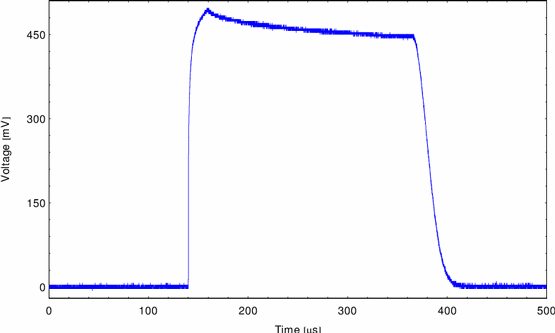 |
Der Spannungsverlauf für dieses Experiment gliedert sich in
- Nullinie (bis ca. 140
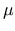 s)
s)
- Aufladen der Membran durch einen 20
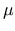 s Spannungspuls über
50
s Spannungspuls über
50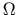 Parallelwiderstand (von 140-160
Parallelwiderstand (von 140-160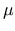 s)
s)
- Entladung der Membran über 10M
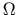 Parallelwiderstand
(160-370
Parallelwiderstand
(160-370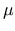 s)
s)
- Durchbruch, Abfließen der Ladungen über den Defekt(370-410
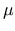 s)
s)
- Nullinie (410
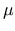 s nach Versuchsbeginn),
s nach Versuchsbeginn),
Nach Applizieren des Spannungspulses
hat die Membran noch eine gewisse Lebensdauer bis zum irreversiblen
Durchbruch. Entgegen der in [35] vorgeschlagenen Verteilung gibt es
in meinen Messungen keine erkennbare Tendenz. Zwischen sofortigen Aufreißen
und einer Relaxationszeit von bis zu 3ms liegen die Werte willkürlich
gestreut. Häufungspunkte sind die ersten 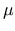 s nach dem Spannungspuls und
Zeiten im ms Bereich. Für diese Verhalten konnte ich keine Erklärung finden.
s nach dem Spannungspuls und
Zeiten im ms Bereich. Für diese Verhalten konnte ich keine Erklärung finden.
Das Auswerten des Spannungsverlaufes mit Meßgleichung 10 zeigt ein
lineares Anwachsen des Defektradius in der Zeit (Abbildung 14),
Abbildung:
Leitfähigkeit G(t), Porenradius a(t) in 1M KCl
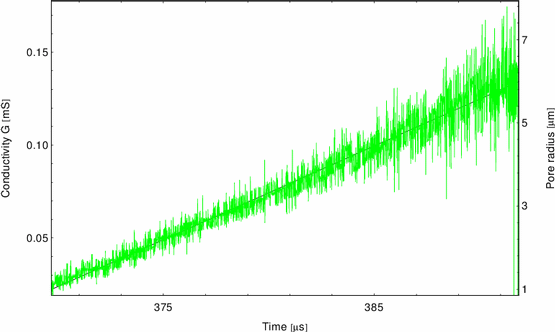 |
und entspricht dem in Abschnitt 2.3.2 betrachteten
trägheitskontrollierten Mechanismus für die Kinetik der
Defektausweitung. Unter 370mV Transmembranspannung beträgt der elektrische
Beitrag zur Oberflächenspannung weniger als zehn Prozent
(Gleichung 6,
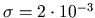 N/m, d=6nm). Damit läßt
sich Gleichung 24 ohne elektrische zeitabhängige Korrekturen zur
Oberflächenspannung verwenden.
N/m, d=6nm). Damit läßt
sich Gleichung 24 ohne elektrische zeitabhängige Korrekturen zur
Oberflächenspannung verwenden.
Für Membranen aus DPh-PC erhält man als radiale Ausdehnungsgeschwindigkeit
eines Defektes v=(0,19 0,02)m/s. Das deckt sich mit den in [40]
gemessenen v=(0,21
0,02)m/s. Das deckt sich mit den in [40]
gemessenen v=(0,21 0,05)m/s.
0,05)m/s.
Über die Ionenstärke des Elektrolyts kann man die Zeit beeinflussen, die das
Aufweiten der Pore beobachtbar bleibt. Hierzu eine quantitative Analyse: Je
niedriger die Ladungsträgerkonzentration des Elektrolyten, desto länger
dauert der Ladungstransport über die Membran. Nach dem Ohmschen Gesetz gilt:
wenn man während des beobachtbaren Aufreißprozesses C als konstant
annimmt. Die Leitfähigkeit G(t) wird wie in Abschnitt 2.2 als
Eingangsleitfähigkeit der Pore mit dem Radius a(t) gewählt:
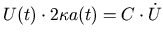 |
(26) |
Der Radius a(t) ist eine lineare Funktion der Zeit, v die konstante
Geschwindigkeit des Aufreißens. Bei 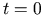 ist
ist 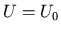 , die
Durchbruchspannung, für
, die
Durchbruchspannung, für
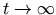 geht U gegen 0. U wird
für das lineare Aufreißen beschrieben durch
geht U gegen 0. U wird
für das lineare Aufreißen beschrieben durch
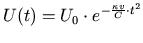 |
(27) |
Gesucht ist die Zeit T, in der U auf 1% des Ausgangswertes abfällt:
Messungen an DPh-PC Membranen ergaben bei verschiedenen
Elektrolytkonzentrationen c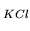 die Zeiten T in Tabelle 1.
die Zeiten T in Tabelle 1.
Tabelle:
Beobachtbares Zeitfenster des Aufreißens
c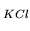 [mM] [mM] |
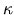 [S/m] [S/m] |
T(U
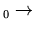 0,01 0,01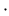 U U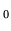 ) [ ) [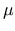 s] s] |
| 10 |
0,14 |
436 |
| 100 |
1,3 |
126 |
| 500 |
6,5 |
61 |
| 1000 |
11,2 |
34 |
| 3000 |
28 |
23 |
|
Als Nebeneffekt dieser Betrachtungen ergibt sich unter Annahme eines linearen
Anwachsens des Defektradius in der Zeit eine alternative Möglichkeit, die
Geschwindigkeit des Aufreißens zu bestimmen. Die Auftragung von T gegen
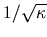 zeigt Abbildung 15.
zeigt Abbildung 15.
Abbildung:
Zeit für das Aufreißen
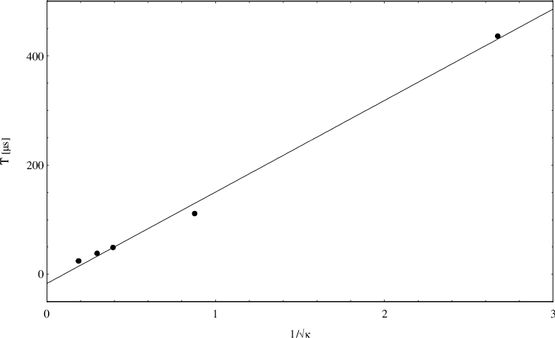 |
Aus dem Anstieg der Regressionsgeraden läßt sich mit Gleichung 30
und einer durchschnittlichen Membrankapazität von (1 0,2)nF die
Aufreißgeschwindigkeit als v=(0,17
0,2)nF die
Aufreißgeschwindigkeit als v=(0,17 0,04)m/s errechnen.
0,04)m/s errechnen.
Eine Abschätzung der erwarteten radialen Ausdehnungsgeschwindigkeit mit
Gleichung 23 ergibt einen um zwei Größenordnungen zu hohen Wert:
Das Molekulargewicht von DPh-PC beträgt 846g/mol. Bei einer Fläche je
Molekül von 0,5nm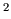 [27] ist die Flächendichte
[27] ist die Flächendichte 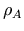 einer
bimolekularen Schicht
einer
bimolekularen Schicht
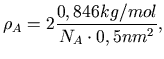 |
(31) |
mit N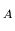 der Avogadrozahl. Mit
der Avogadrozahl. Mit
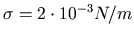 ergibt sich nach
ergibt sich nach
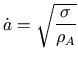 |
(32) |
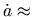 19m/s. In [18,40] wurde die Flächendichte durch
kovalente Bindung von Makromolekülen an einzelne Lipide erhöht. Die
Aufreißgeschwindigkeit ist umgekehrt proportional zur Wurzel aus der
Flächendichte. Da die Oberflächenspannung des Lipidfilmes nicht so einfach
zugänglich ist, liegen keine Daten zum Verhältnis von Reißgeschwindigkeit
und
19m/s. In [18,40] wurde die Flächendichte durch
kovalente Bindung von Makromolekülen an einzelne Lipide erhöht. Die
Aufreißgeschwindigkeit ist umgekehrt proportional zur Wurzel aus der
Flächendichte. Da die Oberflächenspannung des Lipidfilmes nicht so einfach
zugänglich ist, liegen keine Daten zum Verhältnis von Reißgeschwindigkeit
und 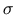 vor. Nach [18,40] läßt sich das lineare Aufreißen
reiner Lipidfilme durch das Einfügen eines konstanten Faktors
vor. Nach [18,40] läßt sich das lineare Aufreißen
reiner Lipidfilme durch das Einfügen eines konstanten Faktors 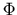 in
Gleichung 23 beschreiben:
in
Gleichung 23 beschreiben:
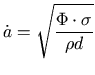 |
(33) |
Die Theorie in Abschnitt 2.3 berücksichtigt keine
temperaturabhängigen entropischen Energiebeiträge zur Stabilität der
Membran. In [27] werden Defekte mit nicht kreisrunden Rändern
betrachtet. Die Membran wird mit einem Netzwerk von Massepunkten
simuliert. Massepunkte sind mit den nächsten Nachbarn über flexible
Bindungen gekoppelt. Bindungen können reißen oder neu entstehen. Es bildet
sich eine Verbindungskonstante z aus, die in [27] nicht näher
definiert wurde. Behandelt man die Randlinie des Defektes als geschlossenen
selbstvermeidenden Pfad von n Schritten der Länge b, beträgt die Anzahl
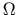 der möglichen Zustände dieses Ringes
der möglichen Zustände dieses Ringes
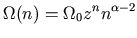 |
(34) |
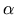 ist ein konstanter Exponent,
ist ein konstanter Exponent, 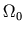 ein von n unabhängiger
Vorfaktor. Der Beitrag zur freien Energie der Membran ist damit
ein von n unabhängiger
Vorfaktor. Der Beitrag zur freien Energie der Membran ist damit
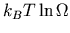 , in erster Näherung proportional zu
n. Gleichung 3 läßt sich auf
, in erster Näherung proportional zu
n. Gleichung 3 läßt sich auf
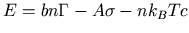 |
(35) |
erweitern. Diese grobe Abschätzung mit der Konstanten c wird erst nach
Anpassung der Simulationsergebnisse an die natürlichen Einheiten von
Lipidmembranen interessant, da jetzt die Fläche A nicht mehr als Kreisfläche
des Defekts errechnet werden darf . Wird die simulierte Membran instabil,
ist die Energiebarriere gegen Defektausweitung nicht mehr vorhanden.
Der entropischen Beitrag zur Randenergie muß den mechanischen
Beitrag gerade aufheben. Die so berechnete Größenordnung des entropischen
Effektes entspricht bei Raumtemperatur einer Randenergie von
9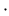 10
10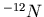 .
.
Es werden allgemeine Aussagen zur Rolle der Entropie bei der
Defektausweitung in Lipidmembranen getroffen. Ist das Lipid in der fluiden
Phase, kann man folgende Effekte erwarten:
- Bei niedriger Temperatur bilden sich kreisrunde Löcher aus,
- bei höherer Temperatur Löcher mit fraktalem Rand.
- Die Energiebarriere gegen Defektbildung aus dem Beitrag der Randenergie
in Membranen unter Spannung kann bei hohen Temperaturen verschwinden.
Temperaturskala und damit Verhalten richten sich nach der Fluidität der
Lipidmoleküle im Bilayer.
Lysolecithin
Lipidmoleküle in dichten Packungen verhalten sich je nach Molekülform
unterschiedlich. Das Verhältnis zwischen der Größe der polaren Kopfgruppe
und dem Umfang des hydrophoben Fettsäureschwanzes bestimmt die Energie, die
zur Krümmung einer Fläche aus diesem Lipid nötig ist. Das verwendete
Lysolecithin besteht aus der gleichen Kopfgruppe wie das DPh-PC, besitzt aber
nur eine Fettsäurekette. Damit setzt es als Zusatz zur membranformenden
Lösung die Energiebarriere gegen spontane Krümmung des Bilayers
herab [5,1]. Es hat Einfluß auf die Randenergie 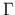 in
Formel 3. Tabelle 2 enthält nach [5] Werte
für PC-Membranen.
in
Formel 3. Tabelle 2 enthält nach [5] Werte
für PC-Membranen.
Tabelle:
Oberflächenspannungen und Randenergien
| Lipid |
![$ \Gamma \ [10^{-11}N]$](img100.png) |
![$ \sigma \ [10^{-3}N/m]$](img101.png) |
| PC in Decan |
0,86 0,04 0,04 |
1,0 0,3 0,3 |
| PC in Decan |
|
|
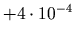 mg/ml LPC mg/ml LPC |
0,33 0,06 0,06 |
0,2 0,1 0,1 |
|
Für Bilayer aus DPh-PC gibt es keine entsprechenden Meßwerte. Sie sollten
sich aber bei Zusatz von Lysolecithin ähnlich verhalten. Die Randenergie ist
nach [5] eine mit dem Gehalt an Lysolecithin lineare Funktion. Mit
Mischungen von DPh-PC und Lysolecithin in verschiedenen Anteilen
durchgeführte Experimente zeigen Veränderungen in der Durchbruchspannung der
Lipiddoppelschicht (Tabelle 3),
Tabelle:
Veränderungen in der Durchbruchsspannung
| |
0,15M KCl |
1M KCl |
| |
U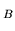 |
d/dt(r) |
U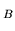 |
d/dt(r) |
| |
[mV] |
[m/s] |
[mV] |
[m/s] |
| DPh-PC |
330 30 30 |
0,19 0,02 0,02 |
430 50 50 |
0,20 0,01 0,01 |
| DPh-PC + 1% Lyso |
|
|
440 40 40 |
0,20 0,02 0,02 |
| DPh-PC + 4% Lyso |
310 30 30 |
0,21 0,02 0,02 |
350 50 50 |
0,19 0,02 0,02 |
| DPh-PC + 8% Lyso |
270 30 30 |
0,23 0,03 0,03 |
320 10 10 |
0,19 0,02 0,02 |
|
die mit Gleichung 5 erklärt werden können. Das Herabsetzen der
mechanischen Randenergie führt zum Ausgleich des mechanischen Anteils mit dem
elektrischen Beitrag bei niedrigeren Spannungen. Rand- und damit Defektbildung
werden für kleinere Spannungen wahrscheinlicher. Nicht nachvollziehen läßt
sich die Herabsetzung der Oberflächenspannung des Bilayers. Da die
Aufreißgeschwindigkeit wesentlich von der Oberflächenspannung bestimmt wird,
müßte sich das Absenken auf ein Fünftel wesentlich auf die Kinetik
auswirken. Die Meßwerte der Aufreißgeschwindigkeit unterscheiden sich aber
nur wenig von denen aus entsprechenden Messungen an reinen DPh-PC Membranen.
Actin
Actinfilamente sind wichtiger Zellbestandteil. Sie bilden mit anderen
filamentösen Strukturen zusammen die Grundlage für Stabilität und
Bewegungsfähigkeit von Zellen. Abbildung 16 zeigt einen
Fibroblasten mit gekennzeichnetem Actingerüst. Die Filamente wurden mit
fluoreszensmarkierten Actinantikörpern für die Fluoreszensmikroskopie
sichtbar gemacht.
Abbildung:
Actingerüst eines Fibroblasten [12]
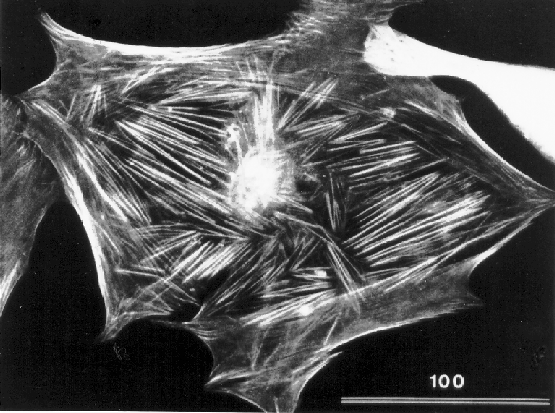 |
Der Balken entspricht 100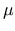 m.
m.
Actinmonomere polymerisieren ab einer kritischen Salzkonzentration in der
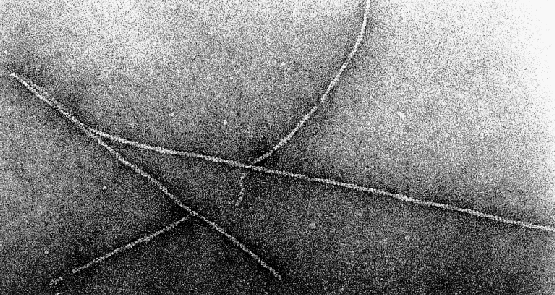
umgebenden Lösung zu Filamenten. Abbildung 17 zeigt ein während
meines Elektronenmikroskopiepraktikums aufgenommenes Bild.
Abbildung 17:
Actinfilamente
 |
Das Polymerisieren ist reversibel. Sinkt die Salzkonzentration unter den
kritischen Wert, zerfallen die Filamente zu Monomeren.
Nach der in [19] beschriebenen Prozedur zur Polymerisation von Actin
an Lipidmembranen wurden auf den dort verwendeten Liposomen zwei
unterschiedliche Anordnungen der Actinfilamente festgestellt:
- zweidimensionaler Kristall
- Netzwerk
Die Actinfilamente entsprachen in beiden Fällen in Struktur und Aufbau dem in
biologischen Systemen vorkommenden F-Actin. Auch die im zweidimensionalen
Kristall angeordneten Filamente bildeten die longitudinale Periodizität
der aufeinanderfolgenden Monomere von 37,5nm aus.
Durchbruchexperimente mit an die Lipiddoppelschicht polymerisiertem Actin
ergeben eine deutliche Änderung in der Kinetik der
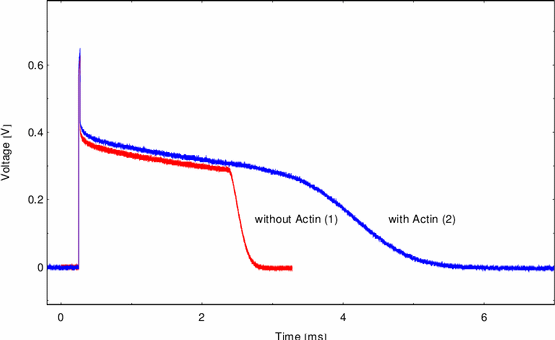
Defektausweitung. Abbildung 18 zeigt Meßkurven für den
Durchbruch einer Membran aus DPh-PC und 10% Stearylamine ohne Zugabe von
Actin und mit Zugabe von Actin auf einer Seite der Küvette.
Abbildung 18:
Durchbruch DPh-PC + 10% Stearylamine
 |
Ohne Actin entspricht das Aufreißen dem schon bei reinen DPh-PC-Membranen
betrachteten trägheitskontrollierten Vorgang. Die Geschwindigkeit der
radialen Ausdehnung des Defektes beträgt v=(0,23 0,1)m/s
(Abbildung 19).
0,1)m/s
(Abbildung 19).
Abbildung:
Lineares Aufreißen DPh-PC + 10% Stearylamine
 |
Mit Actin kommt es in Abbildung 18, Kurve 2, zu einer
drastischen Änderung. Der Ladungsausgleich über den Membrandefekt nimmt mehr
Zeit in Anspruch. Nach Gleichung 30 nimmt der Radius des Defektes
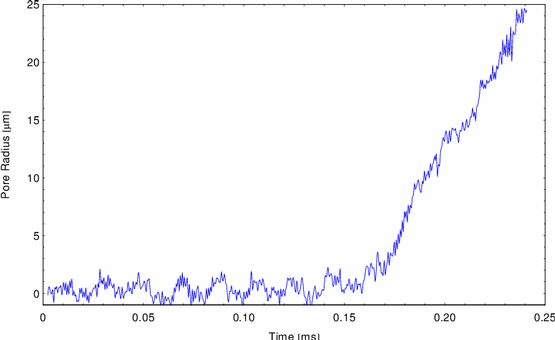
mit einer niedrigeren Geschwindigkeit zu. Abbildung 20 zeigt einen
weiteren Aspekt. Das Anwachsen des Porenradius ist nicht mehr linear in der
Zeit, sondern exponentiell.
Abbildung:
Exponentielles Aufreißen DPh-PC + 10% Stearylamine + Actin
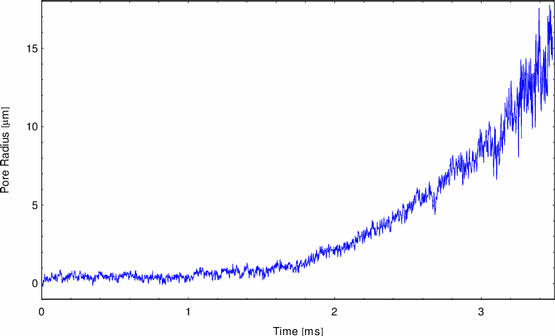 |
Dieses Verhalten läßt sich mit dem in Gleichung 19 vorgestellten
viskositätsbestimmten Aufreißen erklären. Logarithmieren der Kurve in y
ergibt eine Gerade. Der Anstieg m dieser Gerade entspricht nach
Gleichung 19
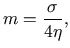 |
(36) |
woraus sich mit einer Oberflächenspannung von 2
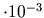 N/m Werte für
die Viskosität des Lipidfilmes mit Actingerüst errechnen lassen:
N/m Werte für
die Viskosität des Lipidfilmes mit Actingerüst errechnen lassen:
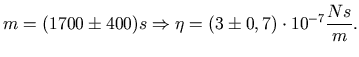 |
(37) |
In [15] ist die Viskosität der Zellmembran von Erythrozyten mit
Theterbildung an Mikropipetten gemessen worden. Das Ergebnis von
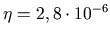 Ns/m unterscheidet sich von meinem Meßwert um eine
Größenordnung. [32] gibt
Ns/m unterscheidet sich von meinem Meßwert um eine
Größenordnung. [32] gibt
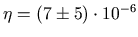 Ns/m bei
25
Ns/m bei
25 C an. Das direkt an die Membran polymerisierte Actin entspricht
nicht dem biologischen Vorbild mit in der Lipidschicht verankerten Proteinen,
von deren Actinbindungsstellen aus sich das Polymernetzwerk
aufspannt. [19] gibt keine Meßwerte für die Oberflächenviskosität
der modifizierten Liposome an. Interessant ist der hier sichtbare Übergang vom
trägheits- zum viskositätskontrollierten Mechanismus des Aufreißens.
C an. Das direkt an die Membran polymerisierte Actin entspricht
nicht dem biologischen Vorbild mit in der Lipidschicht verankerten Proteinen,
von deren Actinbindungsstellen aus sich das Polymernetzwerk
aufspannt. [19] gibt keine Meßwerte für die Oberflächenviskosität
der modifizierten Liposome an. Interessant ist der hier sichtbare Übergang vom
trägheits- zum viskositätskontrollierten Mechanismus des Aufreißens.
Die Stabilität der Lipidmembran gegenüber dem elektrischen Feld wird durch
die Stützstruktur nicht erhöht. Die kritische Spannung lag für DPh-PC
Membranen mit 10% Stearylamine bei (350 90)mV. Nach Polymerisieren des
Actins an die Membran lag die Durchbruchsspannung bei (290
90)mV. Nach Polymerisieren des
Actins an die Membran lag die Durchbruchsspannung bei (290 30)mV und damit
im Rahmen der bei diesen Experimenten großen Streuung der Meßwerte.
30)mV und damit
im Rahmen der bei diesen Experimenten großen Streuung der Meßwerte.
Die hier vorgestellten Daten sind in [22] veröffentlicht.


Nächste Seite: Programmierung
Aufwärts: Dynamik von Defekten in
Vorherige Seite: Material und Methoden
Marcus Lindemann
2001-09-10

![]() , der
Elektrolyt bestand aus 1M KCl. Die Kurve zeigt das Verhalten eines RC-Gliedes
mit 0,93nF als Kapazität des Kondensators. Die Kapazitätsmessung diente
zusätzlich der Qualitätskontrolle. Zu kleine Kapazitäten weisen auf nicht
zum Bilayer ausgedünnte Teile des Lipidfilmes hin. Wenn die Werte nach einer
gewissen Wartezeit nicht im Bereich der üblichen 0,8nF bis 1,2nF lagen, wurde
das Experiment mit einer neuen Membran wiederholt.
, der
Elektrolyt bestand aus 1M KCl. Die Kurve zeigt das Verhalten eines RC-Gliedes
mit 0,93nF als Kapazität des Kondensators. Die Kapazitätsmessung diente
zusätzlich der Qualitätskontrolle. Zu kleine Kapazitäten weisen auf nicht
zum Bilayer ausgedünnte Teile des Lipidfilmes hin. Wenn die Werte nach einer
gewissen Wartezeit nicht im Bereich der üblichen 0,8nF bis 1,2nF lagen, wurde
das Experiment mit einer neuen Membran wiederholt.
![]() 0,02)m/s. Das deckt sich mit den in [40]
gemessenen v=(0,21
0,02)m/s. Das deckt sich mit den in [40]
gemessenen v=(0,21![]() 0,05)m/s.
0,05)m/s.
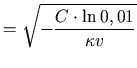
![]() zeigt Abbildung 15.
zeigt Abbildung 15.
![]() [27] ist die Flächendichte
[27] ist die Flächendichte ![]() einer
bimolekularen Schicht
einer
bimolekularen Schicht
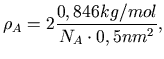
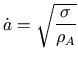
![]() der möglichen Zustände dieses Ringes
der möglichen Zustände dieses Ringes
![]() 90)mV. Nach Polymerisieren des
Actins an die Membran lag die Durchbruchsspannung bei (290
90)mV. Nach Polymerisieren des
Actins an die Membran lag die Durchbruchsspannung bei (290![]() 30)mV und damit
im Rahmen der bei diesen Experimenten großen Streuung der Meßwerte.
30)mV und damit
im Rahmen der bei diesen Experimenten großen Streuung der Meßwerte.