

Nächste Seite: Material und Methoden
Aufwärts: Dynamik von Defekten in
Vorherige Seite: Einleitung
Unterabschnitte
Lipide sind amphiphile Moleküle. Die Kopfgruppen sind wasserlöslich,
hydrophil, wogegen die hydrophoben Fettsäurereste eine Ölphase
bilden. Lipidmoleküle richten sich spontan aus, um in den thermodynamisch
günstigeren Zustand niedrigerer freier Energie zu kommen. Es kommt zur
Grenzflächenbildung. In Lipid-Wasser Gemischen bilden sich Mizellen, Vesikel,
lamellare Phasen oder kompliziertere Strukturen. Tien [29]
gibt eine Abschätzung für die Größenordnung des hydrophoben Effektes
an. Das Mengenverhältnis von Lipidmolekülen mit der Kopfgruppe zum Öl
zeigend zu Molekülen mit der Kopfgruppe zum Wasser zeigend ist ungefähr
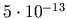 . Die Bildung eines bimolekularen Filmes bedeutet die
Reduktion bzw. Vermeidung von Kontaktfläche zwischen wäßriger und
Kohlenwasserstoffphase und die Maximierung der Kontaktfläche zwischen Wasser
und polaren Kopfgruppen. Der Bilayer ist ein selbstorganisierendes System.
. Die Bildung eines bimolekularen Filmes bedeutet die
Reduktion bzw. Vermeidung von Kontaktfläche zwischen wäßriger und
Kohlenwasserstoffphase und die Maximierung der Kontaktfläche zwischen Wasser
und polaren Kopfgruppen. Der Bilayer ist ein selbstorganisierendes System.
Steht die Lipiddoppelschicht unter Spannung, z.B. durch adhäsives Aufspannen
über ein Loch in einer Teflonwand, oder durch osmotischen Druck in einer
Zelle, wird der Zustand des Bilayers metastabil. Nach Bildung eines initialen
Defektes gelangt die Lipidschicht in einen stabilen Zustand [35]. Das
kann heißen, daß der Lipidfilm bis zum Ausgleich des osmotischen Druckes
eine stabile, wieder verheilende Pore ausbildet [41], oder daß das
Lipid in das Reservoir am Teflonrand des Loches der Meßzelle aufgesogen
wird. Es existieren verschiedene Modelle zur Bildung des initialen Defektes,
der das Aufreißen des Bilayers herbeiführt.
Lipiddoppelschichten haben Leitfähigkeiten von 10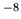 Scm
Scm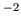 und sind
bis zu Potentialdifferenzen zwischen
und sind
bis zu Potentialdifferenzen zwischen
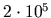 und
und
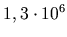 Vcm
Vcm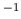 mechanisch stabil [29]. Während die Kopfgruppen von
Wassermolekülen und Ionen des Elektrolytes umgeben sind, bilden die
Kohlenwasserstoffketten eine Energiebarriere gegen die Diffusion von
Ladungsträgern. Nach [26] besteht diese Barriere aufgrund der zu
überwindenden Energiedifferenz beim Übergang der Ionen zwischen Medien
verschiedener Dielektrizitätskonstanten. Für ein Ion des Radius R und der
Ladung q beträgt der Unterschied der Feldenergien
mechanisch stabil [29]. Während die Kopfgruppen von
Wassermolekülen und Ionen des Elektrolytes umgeben sind, bilden die
Kohlenwasserstoffketten eine Energiebarriere gegen die Diffusion von
Ladungsträgern. Nach [26] besteht diese Barriere aufgrund der zu
überwindenden Energiedifferenz beim Übergang der Ionen zwischen Medien
verschiedener Dielektrizitätskonstanten. Für ein Ion des Radius R und der
Ladung q beträgt der Unterschied der Feldenergien
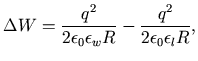 |
(1) |
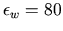 ist die relative Dielektrizitätskonstante des Wassers,
ist die relative Dielektrizitätskonstante des Wassers,
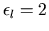 die der Ölphase des Lipids,
die der Ölphase des Lipids,
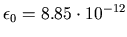 F/m . Kaliumionen haben einen Durchmesser von 151pm, Chloridionen
167pm [16]. Das ergibt für die von mir verwendeten Ionen eine
Größenordnung der Energiedifferenz von
F/m . Kaliumionen haben einen Durchmesser von 151pm, Chloridionen
167pm [16]. Das ergibt für die von mir verwendeten Ionen eine
Größenordnung der Energiedifferenz von 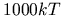 . Es ist beliebig
unwahrscheinlich, daß ein Ion durch die Membran diffundiert.
. Es ist beliebig
unwahrscheinlich, daß ein Ion durch die Membran diffundiert.
Erst durch Defekte, die mit einem polarisierbaren Medium gefüllt sind, wird
der Ionentransport möglich. Diese Poren können von Proteinen gebildet
werden. In reinen Lipidmembranen muß ein wassergefüllter Defekt entstehen.
Mit den mechanische Eigenschaften der Lipiddoppelschicht beschäftigt sich die
Theorie von der Defektbildung aufgrund von Elektrokompression der gesamten
Membran. Die Salzlösung an der Membran wird als elastischer Kondensator
angesehen, der mit der Lipiddoppelschicht als Dielektrikum der relativen
Dielektrizitätskonstante
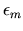 gefüllt ist.
gefüllt ist.
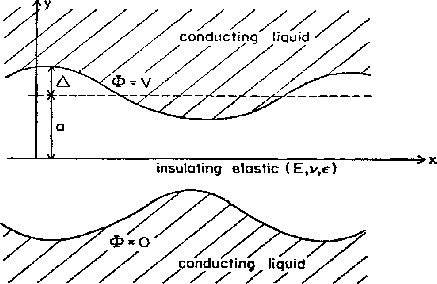
Abbildung 2:
Elastischer Kondensator [8]
 |
Das elektrische Feld übt einen Druck P von
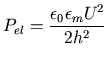 |
(2) |
auf das Dielektrikum aus. U ist die Potentialdifferenz über die
Kohlenwasserstoffphase der Dicke h. Nach Diskussion in [35,42]
müßte die Membrandicke um ca. 39% abnehmen, ehe es zum Durchbruch
kommt. Dickenmessungen haben eine maximale Komprimierbarkeit von 2%
ergeben [23]. Auch die vorhergesagte Durchbruchsspannung ist mit 5V
um eine Größenordnung zu hoch.
Andere Arbeiten wenden die Theorie von [30,31] für induzierte
Dickefluktuationen in dünnen liquiden Filmen auf Bilayer im
elektrischen Feld an [8].
Es muß Arbeit verrichtet werden, um einen planaren Bilayer über die Bohrung
in der Wand der Meßzelle zu spannen. Durch Adhäsionskräfte am Teflon hat
die Membran eine positive Oberflächenspannung 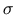 . Ich gehe davon aus,
daß sich in der Membran ein einzelner kreisrunder Defekt
ausweitet [40]. Der Unterschied in der freien Energie zwischen
ungestörter Membran und Membran mit einem Defekt des Radius a ist
. Ich gehe davon aus,
daß sich in der Membran ein einzelner kreisrunder Defekt
ausweitet [40]. Der Unterschied in der freien Energie zwischen
ungestörter Membran und Membran mit einem Defekt des Radius a ist
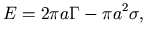 |
(3) |
ohne die Einwirkung des elektrischen Feldes zu
berücksichtigen [10]. 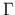 ist die Randenergie des
Lipidfilmes. Ist der Radius a kleiner als der kritische Radius
ist die Randenergie des
Lipidfilmes. Ist der Radius a kleiner als der kritische Radius
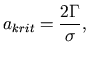 |
(4) |
heilt die Pore wieder zu, ist der Radius größer, reißt die Membran
irreversibel auf.
Der Spannungspuls bewirkt eine Ladungskonzentration mit entgegengesetzten
Vorzeichen an den Lipid-Wasser Grenzflächen. Die elektrische Anziehung dieser
Ladungen äußert sich in einer Kraft auf die Membran, die Korrekturen zu
Randenergie und Oberflächenspannung notwendig macht. In [38,39]
werden die berichtigten Größen mit
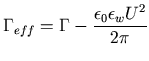 |
(5) |
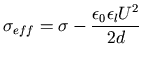 |
(6) |
angegeben, wobei d die Membrandicke darstellt. Typische Oberflächenspannungen
und Randenergien für Bilayer liegen bei
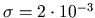 N/m und
N/m und
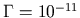 N [5]. Damit erleichtert das elektrische Feld die
Randbildung, während der elektrische Beitrag zur Oberflächenspannung dem
Aufreißen entgegenwirkt. Ist die effektive Randenergie zu Null ausgeglichen,
aber die mechanische Oberflächenspannung überwiegt den elektrischen
Beitrag, kommt es zur Defektbildung und zum irreversiblen Reißen der Membran.
Wechselt die Oberflächenspannung das Vorzeichen, bevor ein Rand entstehen
kann, sollte es zu stabilen Poren in molekularer Dimension kommen. Erst bei
sehr hohen Spannungen treiben Maxwellkräfte den Lipidfilm auseinander.
N [5]. Damit erleichtert das elektrische Feld die
Randbildung, während der elektrische Beitrag zur Oberflächenspannung dem
Aufreißen entgegenwirkt. Ist die effektive Randenergie zu Null ausgeglichen,
aber die mechanische Oberflächenspannung überwiegt den elektrischen
Beitrag, kommt es zur Defektbildung und zum irreversiblen Reißen der Membran.
Wechselt die Oberflächenspannung das Vorzeichen, bevor ein Rand entstehen
kann, sollte es zu stabilen Poren in molekularer Dimension kommen. Erst bei
sehr hohen Spannungen treiben Maxwellkräfte den Lipidfilm auseinander.
Elektrische Leitfähigkeit
Der elektrische Widerstand eines kreisrunden Defekts der Dicke d und des
Radius a in einer isolierenden Schicht setzt sich aus zwei Komponenten
zusammen. Erste Komponente ist der Widerstand R eines mit Elektrolyt gefüllten
Zylinders:
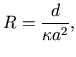 |
(7) |
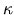 spezifische Leitfähigkeit der Salzlösung. Die zweite
Komponente berücksichtigt den Potentialabfall von einer unendlich entfernten
Elektrode zu einer leitenden Scheibe endlichen Durchmessers. Nach [25]
beträgt deren Eingangswiderstand
spezifische Leitfähigkeit der Salzlösung. Die zweite
Komponente berücksichtigt den Potentialabfall von einer unendlich entfernten
Elektrode zu einer leitenden Scheibe endlichen Durchmessers. Nach [25]
beträgt deren Eingangswiderstand
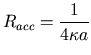 |
(8) |
Der Eingangswiderstand wirkt an jeder Stirnfläche des leitenden
Zylinders.
Zur Auswertung meiner Versuche betrachte ich den Potentialverlauf an der
Membran über der Zeit. Nach dem Ohmschen Gesetz ist
![$\displaystyle G(t)=\frac{I(t)}{U(t)}=\frac{1}{U(t)}\frac{\partial Q(t)}{\partia...
...-\partial [CU(t)]}{\partial t} =\frac{-C}{U(t)}\frac{\partial U(t)}{\partial t}$](img28.png) |
(9) |
Kleine Defektradien haben einen vernachlässigbaren Einfluß auf die
Gesamtkapazität der Membran. Deshalb wird die Kapazität als Konstante
angesehen. Bei Porenradien über 1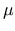 m und der Dicke des Defektes von
ca. 6nm [11] kann man den Widerstandsbeitrag des leitenden Zylinders
gegenüber dem Eingangswiderstand seiner zwei Stirnflächen
unberücksichtigt lassen. Aus 8 und 9 folgt die
Meßgleichung für die Bestimmung des Porenradius
m und der Dicke des Defektes von
ca. 6nm [11] kann man den Widerstandsbeitrag des leitenden Zylinders
gegenüber dem Eingangswiderstand seiner zwei Stirnflächen
unberücksichtigt lassen. Aus 8 und 9 folgt die
Meßgleichung für die Bestimmung des Porenradius
Sie wird zur Auswertung meiner Spannungsverläufe angewendet.
Kinetik
Im statischen Fall wird die aus der Adhäsionskraft des Lipids am
Teflon resultierende Kraft auf die Membran durch die Oberflächenspannung
des Lipidfilms aufgehoben. An der Aufhängung des Bilayers wirkt
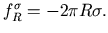 |
(11) |
R ist der Radius des Bilayers. Kommt es zum Aufreißen der
Lipiddoppelschicht, entstehen Kraftbeiträge aus der Trägheitskraft
der beschleunigten Lipidmoleküle und der Scherkraft aufgrund der inneren
Reibung in der Lipiddoppelschicht.
Für die Berechnungen wird die Membran als inkompressibel und homogen
angenommen, der Defekt als kreisrund. Die Dicke der Membran soll sich nicht
ändern. Zu jedem Zeitpunkt t=t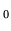 ist damit folgende Gleichung erfüllt:
ist damit folgende Gleichung erfüllt:
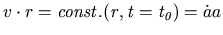 |
(12) |
Da das Produkt aus Radius und radialer Geschwindigkeit über die ganze Membran
konstant sein soll, kann ich als Referenzwerte die Daten am Lochrand
einsetzen.
Belegt man einen inkompressiblen hochviskosen Flüssigkeitsfilm mit Partikeln
und beobachtet das Aufreißen eines Defektes, dann ist zu jedem Zeitpunkt
der gesamte Flüssigkeitsfilm in Bewegung. Die Partikel driften tangential
auseinander [9]. Das führt nach [14,15] zu einer
viskosen Schubspannung von
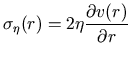 |
(13) |
Aus der Gleichung 12 bekommt man den Ausdruck
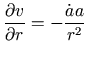 |
(14) |
und kann damit
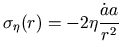 |
(15) |
schreiben. Die differentielle Kraft an einem Punkt der Membran ergibt sich als
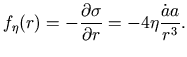 |
(16) |
Die am Rand des Defektes angreifende Kraft erhält man nach Integration über
den verbleibenden Film.
für R a. Da der Film als inkompressibel angenommen wurde und der Defekt so
klein sein soll, daß er die am Rand der Membran wirkenden Kräfte nicht
beeinflußt, kann man in Gleichung 11 den Radius R mit dem Radius a
des Defektes substituieren. Wenn die Scherkräfte alle anderen Beiträge zur
Kinetik des Aufreißens überwiegen, erhält man nach Gleichsetzen
von 11 und 17 die Differentialgleichung
a. Da der Film als inkompressibel angenommen wurde und der Defekt so
klein sein soll, daß er die am Rand der Membran wirkenden Kräfte nicht
beeinflußt, kann man in Gleichung 11 den Radius R mit dem Radius a
des Defektes substituieren. Wenn die Scherkräfte alle anderen Beiträge zur
Kinetik des Aufreißens überwiegen, erhält man nach Gleichsetzen
von 11 und 17 die Differentialgleichung
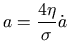 |
(18) |
mit der Lösung
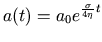 |
(19) |
für das viskositätskontrollierte Aufreißen.
Trägheitskraft
Reine Lipidmembranen haben in der fluiden Phase eine verschwindend kleine
Viskosität. Die Kinetik ihres Aufreißens wird von der Massenträgheit der
Membranmoleküle bestimmt. Bei einer Schallgeschwindigkeit im Lipidfilm von
1400ms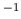 und Durchmessern des Bilayers von
und Durchmessern des Bilayers von 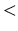 1mm kann man davon
ausgehen, daß das Aufreißen dem gleichen Mechanismus wie im
viskositätsbestimmten Fall folgt: Man muß die Kraft, die nötig ist, ein
Flächenelement zu beschleunigen, über alle Flächenelemente der Membran
aufintegrieren.
1mm kann man davon
ausgehen, daß das Aufreißen dem gleichen Mechanismus wie im
viskositätsbestimmten Fall folgt: Man muß die Kraft, die nötig ist, ein
Flächenelement zu beschleunigen, über alle Flächenelemente der Membran
aufintegrieren.
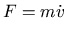 |
(20) |
Mit Gleichungen 12 und 14 ist
da das Kräftegleichgewicht zu jedem Zeitpunkt gelten muß und a sowie
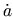 zu einem festen Zeitpunkt Konstanten sind.
zu einem festen Zeitpunkt Konstanten sind.
Aus der Gleichgewichtsbedingung mit Gleichung 11 erhält man
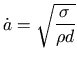 |
(23) |
als die Differentialgleichung für das trägheitskontrollierte Aufreißen. Der
Radius des Defektes ergibt sich als
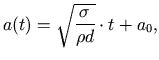 |
(24) |


Nächste Seite: Material und Methoden
Aufwärts: Dynamik von Defekten in
Vorherige Seite: Einleitung
Marcus Lindemann
2001-09-10
![]() Scm
Scm![]() und sind
bis zu Potentialdifferenzen zwischen
und sind
bis zu Potentialdifferenzen zwischen
![]() und
und
![]() Vcm
Vcm![]() mechanisch stabil [29]. Während die Kopfgruppen von
Wassermolekülen und Ionen des Elektrolytes umgeben sind, bilden die
Kohlenwasserstoffketten eine Energiebarriere gegen die Diffusion von
Ladungsträgern. Nach [26] besteht diese Barriere aufgrund der zu
überwindenden Energiedifferenz beim Übergang der Ionen zwischen Medien
verschiedener Dielektrizitätskonstanten. Für ein Ion des Radius R und der
Ladung q beträgt der Unterschied der Feldenergien
mechanisch stabil [29]. Während die Kopfgruppen von
Wassermolekülen und Ionen des Elektrolytes umgeben sind, bilden die
Kohlenwasserstoffketten eine Energiebarriere gegen die Diffusion von
Ladungsträgern. Nach [26] besteht diese Barriere aufgrund der zu
überwindenden Energiedifferenz beim Übergang der Ionen zwischen Medien
verschiedener Dielektrizitätskonstanten. Für ein Ion des Radius R und der
Ladung q beträgt der Unterschied der Feldenergien
![]() gefüllt ist.
gefüllt ist.
![]() . Ich gehe davon aus,
daß sich in der Membran ein einzelner kreisrunder Defekt
ausweitet [40]. Der Unterschied in der freien Energie zwischen
ungestörter Membran und Membran mit einem Defekt des Radius a ist
. Ich gehe davon aus,
daß sich in der Membran ein einzelner kreisrunder Defekt
ausweitet [40]. Der Unterschied in der freien Energie zwischen
ungestörter Membran und Membran mit einem Defekt des Radius a ist
![]() ist damit folgende Gleichung erfüllt:
ist damit folgende Gleichung erfüllt: